[코테 연습] 정수 삼각형 Python

문제

7

3 8

8 1 0

2 7 4 4

4 5 2 6 5

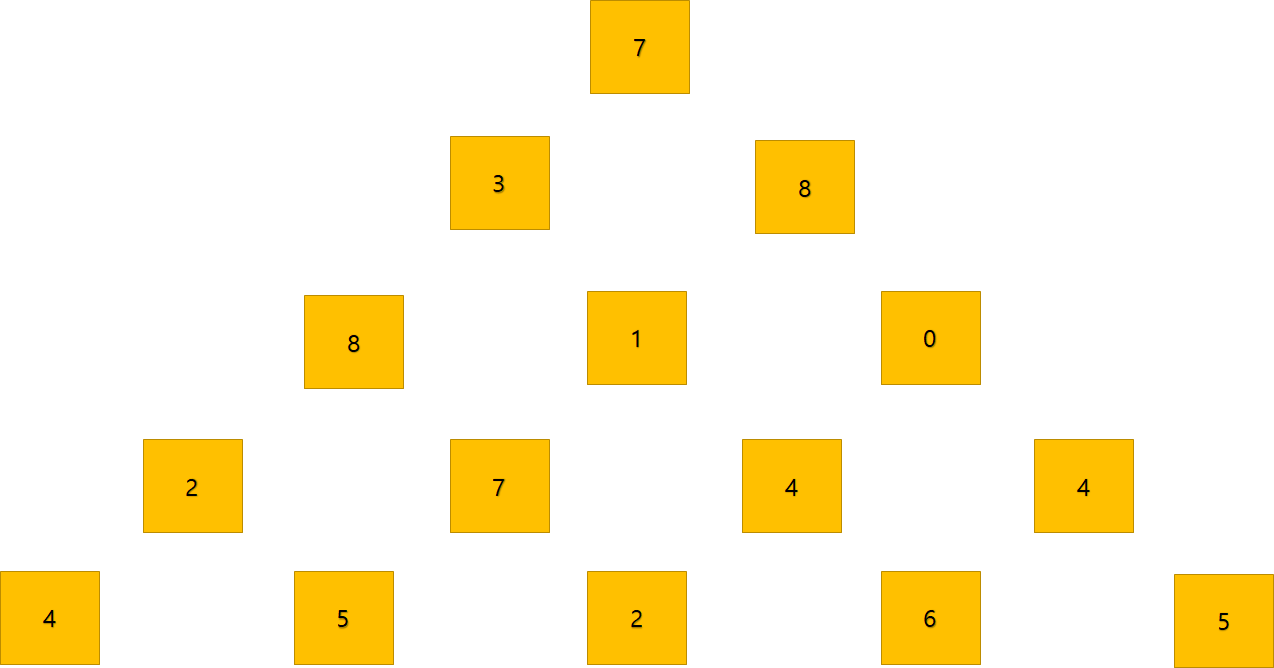
위 그림은 크기가 5인 정수 삼각형의 한 모습이다.

맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.

삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는 모두 정수이며, 범위는 0 이상 9999 이하이다.

 

아래와 같은 삼각형이 있습니다....,,

아니,,  다음과 같은,,

 

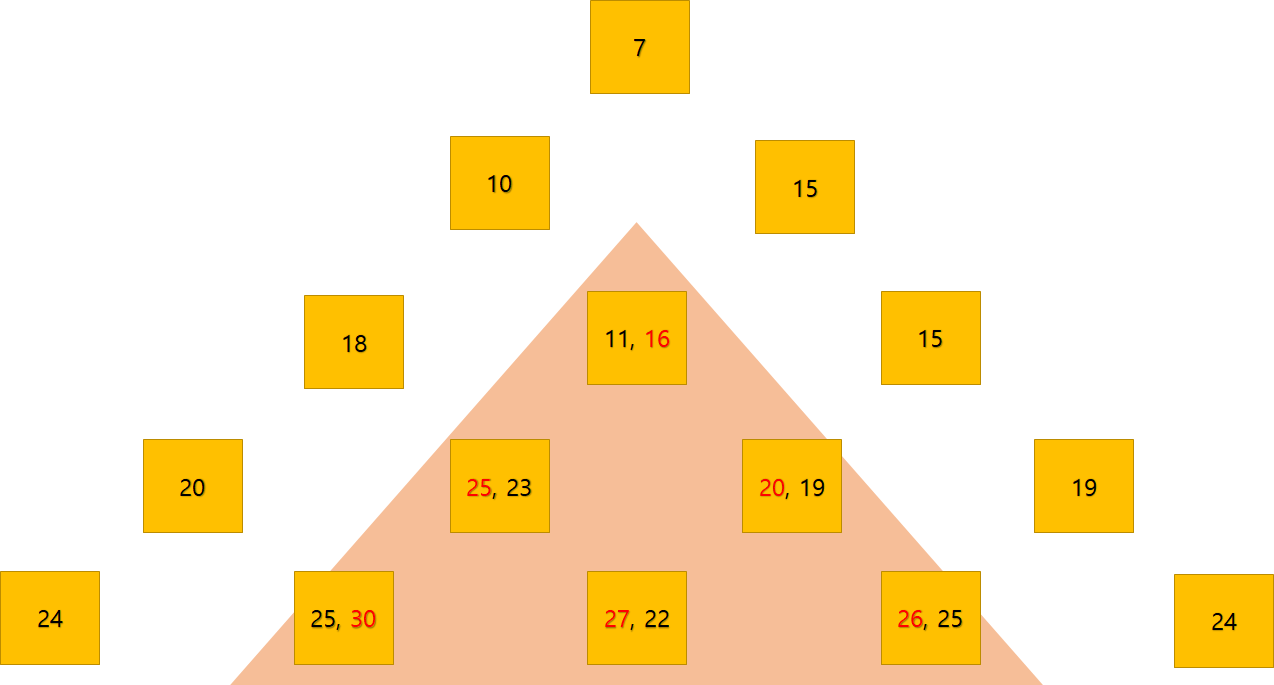
최대 값을 구하기 위해서 최대 값을 지닌 삼각형으로 재탄생 시켜봅니다. 그림을 그리다보면 규칙이 찾아지죠

붉은색으로 표시된 삼각형의 안쪽은 부모 노드로부터 2가지의 값이 생겨나게 되서 둘 중에 큰 값을 선택해야 합니다.

그렇다면,, 함수를 2개 만들어볼까요 

 

 

삼각형을 만들기 위해 배열을 이용해보겠읍니다,, 노드 만들어서 트리로 생성할까했는데,, 그거까지 하면 괜히 insert를 위해서 트리 순회나 해야하기때문에 불필요해 보입니다..

 

 

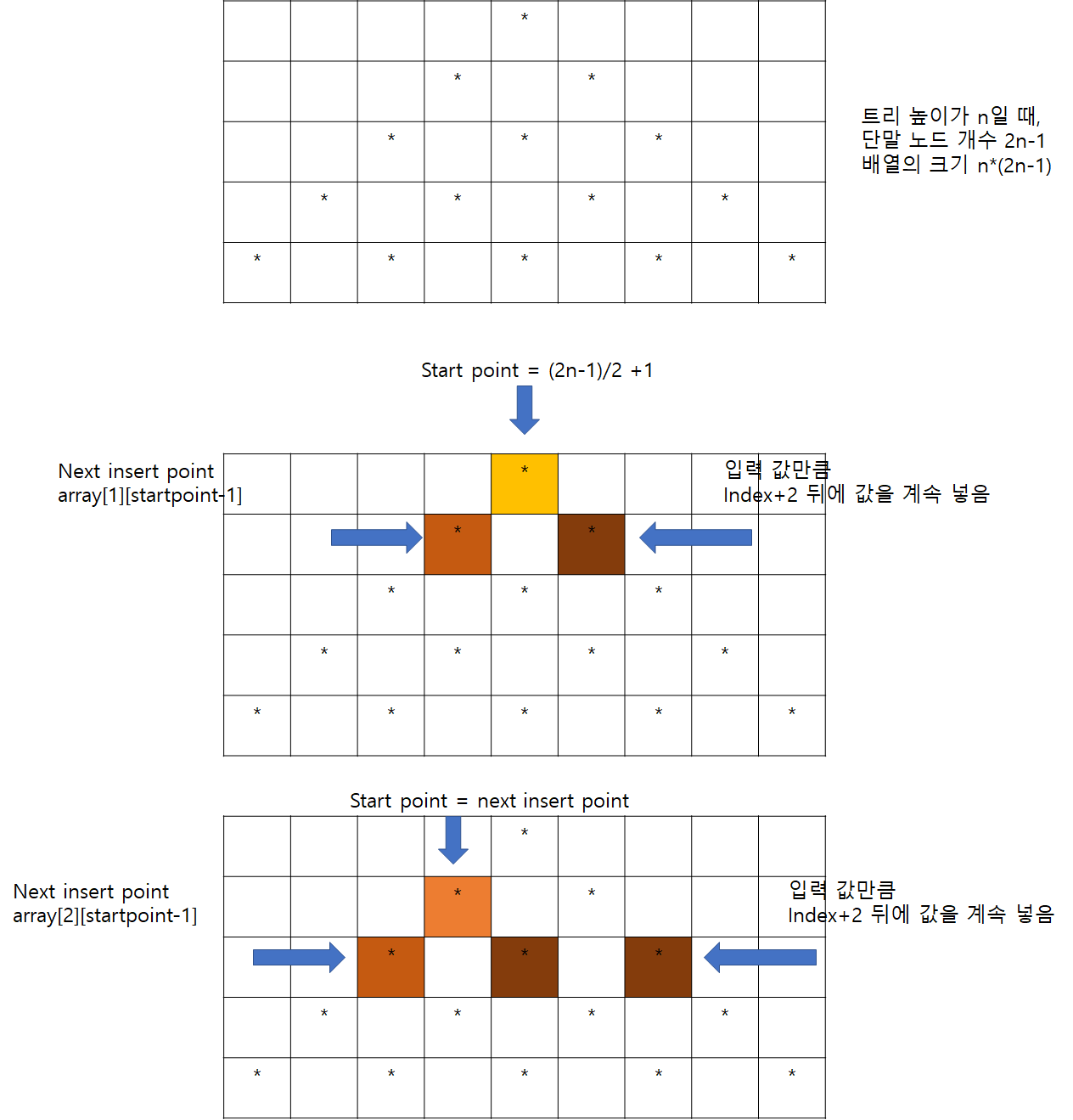
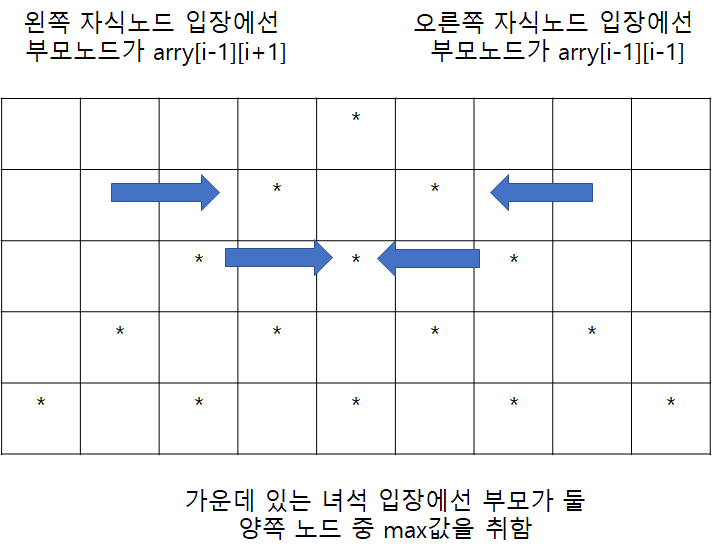
n = int(input())

size = 2 * n - 1  # 단말 노드 크기
maxTri = [[0 for _ in range(size)] for _ in range(n)]

startPoint = int((2 * n - 1) / 2)  # 루트 노드 시작점
maxTri[0][startPoint] = list(map(int, input().split()))[0]

startPoint -= 1
for i in range(1, n):
    num = list(map(int, input().split()))
    nextPoint = startPoint
    numL = len(num)
    for j in range(numL):
        ele = num[j]
        if j == 0:
            maxTri[i][nextPoint] = ele + maxTri[i - 1][nextPoint + 1]

        elif j == numL - 1:
            maxTri[i][nextPoint] = ele + maxTri[i - 1][nextPoint - 1]

        else:
            parents_1 = maxTri[i - 1][nextPoint + 1]
            parents_2 = maxTri[i - 1][nextPoint - 1]

            maxTri[i][nextPoint] = max(ele + parents_1, ele + parents_2)

        nextPoint += 2

    startPoint = startPoint - 1

print(max(map(max, maxTri)))