신경망 학습 #2

손실 함수를 설정하는 이유

 

왜 정확도가 아니라 손실 함수를 지표로 하여 학습을 진행하는 것일까? 

정확도를 지표로 하면 배개변수의 미분이 대부분의 장소에서 0이 되기때문이다.

미분이 0이 되는게 왜?

 

가중치 매개변수의 손실 함수의 미분 : 가중치 매개변수의 값을 아주 조금 변화 시켰을 때, 손실함수가 어떻게 변하는가?

 

매개변수의 값을 조금씩 변화시켜도 정확도는 별 영향을 받지 않음 변해도 불연속적으로 변함

정확도를 지표로 삼으면 값이 불연속적으로 띄엄띄엄 변함 32 -> 33 -> 34%

손실함수를 지표로 삼으면 값이 연속적으로 변함 0.92543.. -> 0.93432..

 

아래 그림을 보면 계단 함수는 대부분의 위치에서 기울기가 0이므로 활성화 함수로 쓰지 않는다. 한번에 값이 확! 바뀜

그에 반해 시그모이드 함수는 0이 안됨 서서..히..변함..

계단 함수

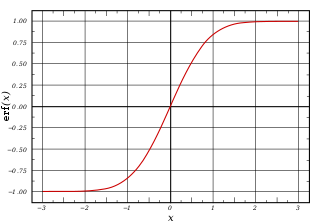
시그 모이드 함수

 

 

수치 미분 : 아주 작은 차분으로 미분

 

마라톤 선수가 10분에서 2km씩 달리면 2/10 = 0.2, 분 당 0.2km라는 뜻

미분 : 특정 순간의 변화량

미분은 아래와 같이 코딩할 수 있다.

구문 에러: 책에 1e라고 나와있는데 1넣으면 에러뜬다 띠용

ln[109]는 수식 그대로 코딩한 내용이다.

h = 10e - 50 : 최대한 h를 한없이 0에 가깝게 하기위해 아주작은 값을 부여함

 

ln[112]는 정확한 구현을 위해 코딩한 내용이다.

h = e-4 : 가령 10e - 50 과 같은 아~주 작은 값을 하면 반올림 오차(소수점 뒤에 몇자리 이하는 생략하는)가 발생함 le - 4가 적절한 값이라고 알려져 있다함

 

 

중심 차분(중앙 차분) : x를 중심으로 그 전후의 차분(임의 두 점에서의 함수 값들의 차이)을 계산

[109]처럼 하면, 그냥 x와 x+h사이의 차이만 구하는거지 진짜 기울기를 구하는게 아니다.

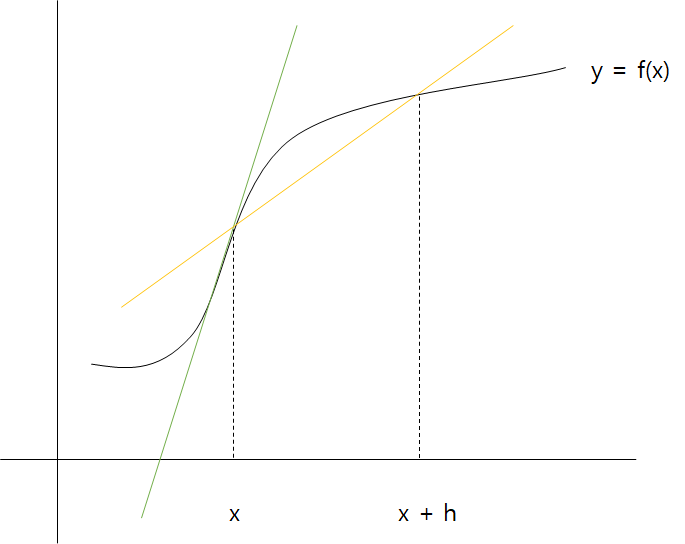
아래 그림을 보면 노란색이 f(x+h)-f(x)이다. 그러나 초록색 선이 진짜 기울기다. 

둘의 오차를 줄이기 위해서 중심 차분을 이용한다. (x+h)와 (x-h)일 때 함수 f의 차분을 계산하는 방법을 사용

 

수치 미분을 사용해보자. 아래와 같이 2차 함수를 하나 만든다. y = 0.01x^2 + 0.1x

 

변화량이 다음과 같이 나온다.  

0.01x^2+0.1x를 미분하면 0.02x+0.1이므로 x=5,0.2 x=10,0.3 정답에 거의 근접하다. 그래프로 그려도 잘 나온다.

 

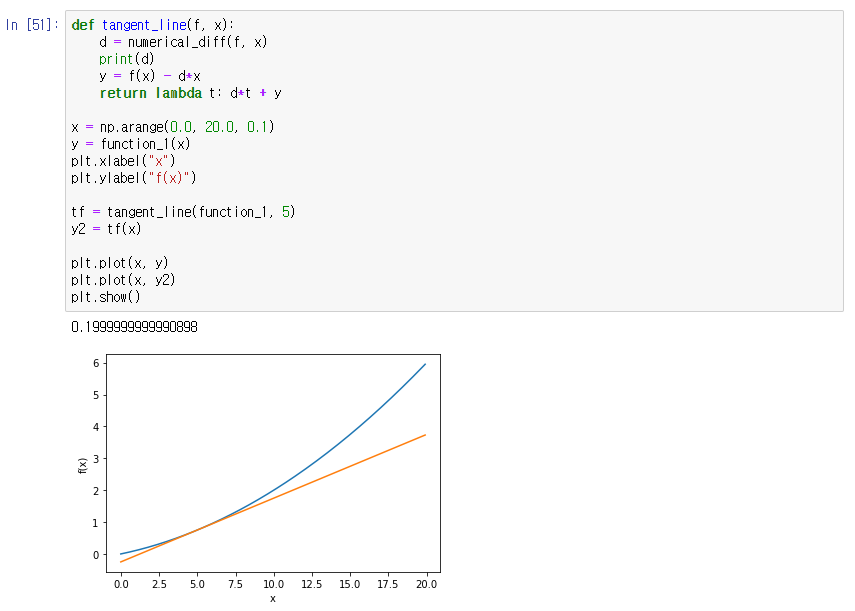
편미분은 다음과 같이 할 수 있다 f(x0, x1) = x0^2 + x1^2가 존재할 때, 두 변수의 값을 각각 고정해놓고 return을 시키는 방식으로 

 

모든 변수의 편미분을 벡터로 정리한 것을 기울기라고 한다. 기울기는 아래와 같이 구할 수 있다.

 

가만 보면, 앞에서 했던거를 똑같이 한다. 변수 개수만큼 반복할 뿐,,

 

https://github.com/WegraLee/deep-learning-from-scratch/blob/master/ch04/gradient_2d.py

WegraLee/deep-learning-from-scratch

위의 링크로 가면 코드를 얻을 수 있다. 아래 그림은 기울기를 나타낸다. 

화살표는 모두 한 곳을 가르키고 있으며 그 곳에 가까워질 수록 작아지고 있다.

기울기가 가르키는 쪽은 각 장소에서 함수의 출력 값을 가장 크게 줄이는 방향이다.

 

경사하강법

일반적인 문제의 손실 함수는 굉장히 복잡하다. 매개변수 공간이 광대해 어디가 최솟값이 되는 곳인지 짐작이 어렵다. 

기울기를 잘 이용해서 함수의 값이 가능한 한 작은 값을 찾으려는 것이 경사하강법의 목적이다.

주의할 점은 실제로 복잡한 함수에서는 기울기가 가리키는 방향에 최솟값이 없는 경우가 대부분이기때문에 그 쪽이 항상 최솟값이라고 보장할 수는 없다.

 

함수는 극솟값, 최솟값, 안장점(saddle point)에서 기울기가 0이다. 

극솟값 : 국소적인 최솟값, 한정된 범위에서의 쵯값인 점 

안장점 : 어느 방향에서 보면 극댓값이고 다른 방향에서 보면 극솟값 

안장점

대부분 복잡하고 찌그러진 모양의 함수라면 평평한 곳으로 파고들면서 고원(plateau)라고 하는 학습 정체기에 빠진다

https://www.codesofinterest.com/2017/04/how-deep-should-deep-learning-be.html

경사 하강법은 현 위치에서 기울어진 방향으로 일정 거리만큼 이동. 이렇게 이동하면서 함수의 값을 점차 줄이는 것이 경사법(최솟값을 찾는 것:경사 하강법, 최댓값을 찾는 것:경사 상승법)

 

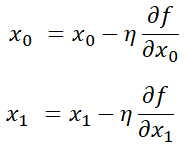
경사 하강법 수식

 

 

위 식에서 에타는 갱신하는 양을 나타내고, 이를 학습률이라고 한다. 한 번의 학습으로 얼마만큼 학습해야할지 (갱신을 얼마나 할지)를 정함 학습률이 너무 크면 값이 발산하고 너무 작으면 거의 갱신되지 않은채로 끝나버린다.

 

학습률같은 매개 변수를 하이퍼파라미터라고 한다. 사람이 직접 설정해야하는 매개변수.

 

아래는 경사법으로 f(x0,x1) = x0^2 + x1^2의 최솟값을 구하는 코드로 결과 값이 거의 (0, 0) 에 가깝다

https://github.com/WegraLee/deep-learning-from-scratch/blob/master/ch04/gradient_method.py

WegraLee/deep-learning-from-scratch

위 링크로 가면 코드가 있다. 코드를 실행시키면 아래와 같은 그래프가 나타난다. 값이 가장 낮은 원점에 점점 가까워지는 것을 확인할 수 있다.

다음은 간단한 신경망으로 실제 기울기를 구하는 코드이다. 우선 사전에 필요한 코드를 작성한다. 모든 코드는 아래 사이트에 있다.

https://github.com/WegraLee/deep-learning-from-scratch

WegraLee/deep-learning-from-scratch

 

아래는 간단한 신경망을 만드는 코드이다. 메서드는 초기화, 예측, 손실 함수의 값을 구하는 메서드로 이루어져 있다.

loss 함수의 x는 입력 데이터 t는 정답 레이블이다.

 

다음은 위의 함수를 이용하여 기울기를 구하는 코드이다.  

net.W는 가중치 매개 변수를 뜻하고.. predict를 이용하여 각 값의 가중치를 예측한 뒤 loss를 이용하여 정답 레이블과 함께 계산하여 손실 값을 계산해낸다. 

In[92]에서 예측 결과 값이 가장 큰 idx가 1이기 때문에  np.array에 정답 레이블을 건내줄  때, idx=1의 값을 1로 지정하여 건낸다.

 

이어서 기울기를 구하면 f(W) 함수는 numerical_gradient 내부에서 f(x)를 실행하는데, 이와의 일관성을 위해 정의한 것으로 W는 dummy로 만든 것이다.

 

 

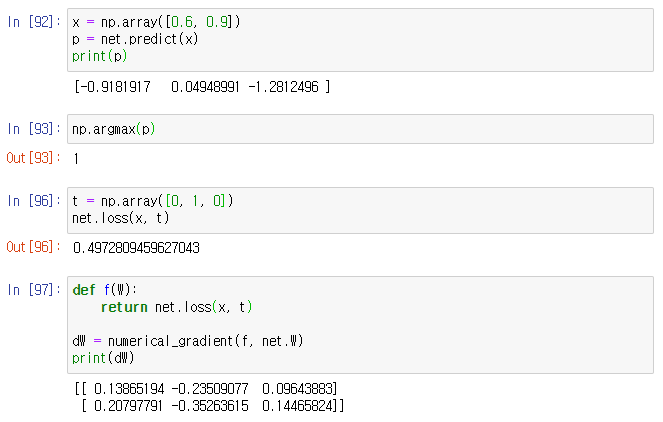
배열의 값을 해석하자면 + 0.1 또는 + 0.3 은 해당 인덱스의 가중치를 h만큼 늘리면 손실함수가 그만큼 증가한다는 것이고 - 0.5 또는 - 0.7은 손실함수가 그만큼 감소한다는 뜻이다. 

그러므로 값을 줄이기 위해선 +는 -의 방향으로 갱신 -는 +의 방향으로 갱신해야함을 알 수 있다. 

그리고 +0.1 보다는 - 0 .5가 갱신되는 양의 기여도가 더 크다는 것을 알 수 있다.

 

f(W)는 다음과같이 람다로 구현할 수 있다.